- 2023/11~ にQuartoからWordPressに移行しました。ざっと修正していますが、修正しきれていない記述などがあれば、コメントでご指摘いただけますと嬉しく思います。
確率分布
確率分布は、多分、統計を学ぶにあたって困る最初の壁だと思います。ここでは、イメージをしっかりと持ってもらったうえで、代表的な確率分布である正規分布について説明してあります。(尚、イメージについては、かえって訳が分からなくなる可能性もありますので、その点ご了解してくださると幸いです。)
先にお断り
私自身は統計学を大学で学んでいた等は「まったくありません」。
確実に専門家の方からおしかりを受ける内容が含まれていると思っておりますので、くれぐれも本ブログの情報を主にすることがないように、よろしくお願い申し上げます。(きちんとした成書を参考にしてください。)また、致命的な間違い等を発見された方はお教えいただけると嬉しく思います。
状況設定
皆さんの手元にサイコロが二つあるとします。
実は、このサイコロ、一つはいかさまに使われるサイコロで、3と2が他の数字より出やすく細工されてあります。
見た目では二つのサイコロは、見分けがつきません。
どのように見分けますか?
試しに10000回ずつ振ってみて、その結果をグラフにしてみましょう。
(こっそり答えを先にお教えすると、サイコロ1が公平なサイコロ、サイコロ2がいかさまサイコロです)
library(tidyverse)
roll1 <- function(){
sample(1:6,1)
}
roll2 <- function(){
sample(1:6,1,prob = c(2,3,3,1,1,2))
}
result1 <- map_int(1:1000,~{roll1()})
result2 <- map_int(1:1000,~{roll2()})dice1 <- ggplot() +
geom_bar(aes(x = result1)) +
labs(x = "サイコロ1の結果", y = "回数")
dice2 <- ggplot() +
geom_bar(aes(x = result2)) +
labs(x = "サイコロ2の結果", y = "回数")
cowplot::plot_grid(dice1,dice2)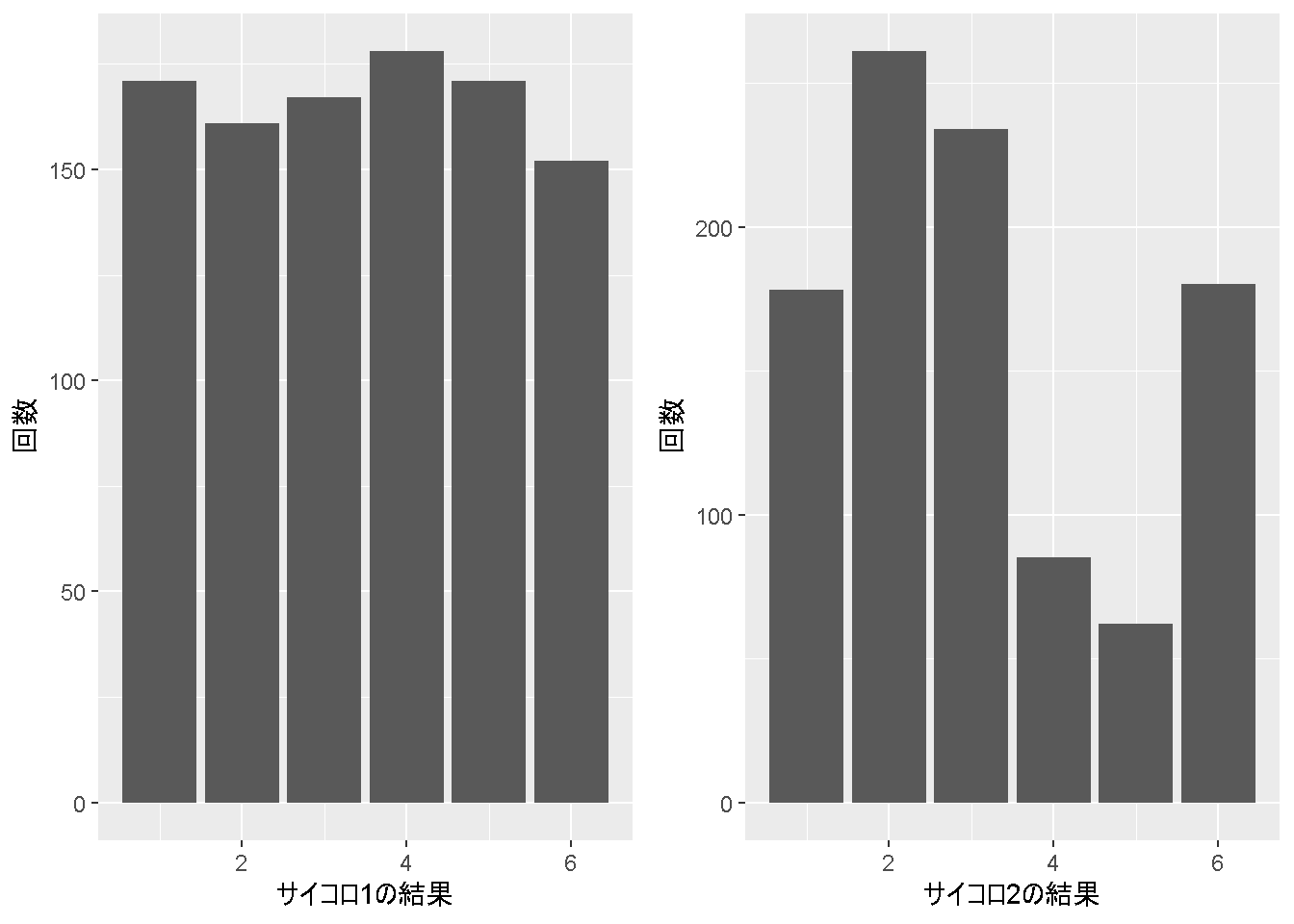
どうでしょうか?
見た目だけでも、サイコロ1の結果のほうが正しいサイコロっぽいですよね?
表にするとサイコロ1は、
hyou1 <- result1 %>%
enframe() %>%
count(value)
hyou1 %>%
rename(`出目` = value,
`回数` = n) %>%
knitr::kable()| 出目 | 回数 |
|---|---|
| 1 | 171 |
| 2 | 161 |
| 3 | 167 |
| 4 | 178 |
| 5 | 171 |
| 6 | 152 |
サイコロ2は、
hyou2 <- result2 %>%
enframe() %>%
count(value)
hyou2 %>%
rename(`出目` = value,
`回数` = n) %>%
knitr::kable()| 出目 | 回数 |
|---|---|
| 1 | 178 |
| 2 | 261 |
| 3 | 234 |
| 4 | 85 |
| 5 | 62 |
| 6 | 180 |
となります。
ここまで、すべて回数で説明してきていますが、サイコロ1が3と出る確率を、$P(X_1=3)$と書くとすると、サイコロdの出目がnとなる確率は、$P(X_d=出目)$とかけます。これを表で表現するとすると、
サイコロ1は、
hyou1_2 <- hyou1 %>%
mutate(total = sum(n)) %>%
mutate(p = n/total)
hyou1_2 %>%
knitr::kable(digits = 2, col.names = c("出目","回数","総試行回数","$P(X_1=出目)$"))| 出目 | 回数 | 総試行回数 | $P(X_1=出目)$ |
|---|---|---|---|
| 1 | 171 | 1000 | 0.17 |
| 2 | 161 | 1000 | 0.16 |
| 3 | 167 | 1000 | 0.17 |
| 4 | 178 | 1000 | 0.18 |
| 5 | 171 | 1000 | 0.17 |
| 6 | 152 | 1000 | 0.15 |
サイコロ2は、
hyou2_2 <- hyou2 %>%
mutate(total = sum(n)) %>%
mutate(p = n/total)
hyou2_2 %>%
knitr::kable(digits = 2, col.names = c("出目","回数","総試行回数","$P(X_2=出目)$"))| 出目 | 回数 | 総試行回数 | $P(X_2=出目)$ |
|---|---|---|---|
| 1 | 178 | 1000 | 0.18 |
| 2 | 261 | 1000 | 0.26 |
| 3 | 234 | 1000 | 0.23 |
| 4 | 85 | 1000 | 0.09 |
| 5 | 62 | 1000 | 0.06 |
| 6 | 180 | 1000 | 0.18 |
となります。
ここで、計算した、$P(X_d=出目)$をグラフに表示してみると
bind_rows(
hyou1_2 %>% mutate(dice = "サイコロ1"),
hyou2_2 %>% mutate(dice = "サイコロ2")
) %>%
ggplot() +
geom_col(aes(x = value, y = p)) +
facet_wrap(~dice) +
labs(x = "出目", y = "確率")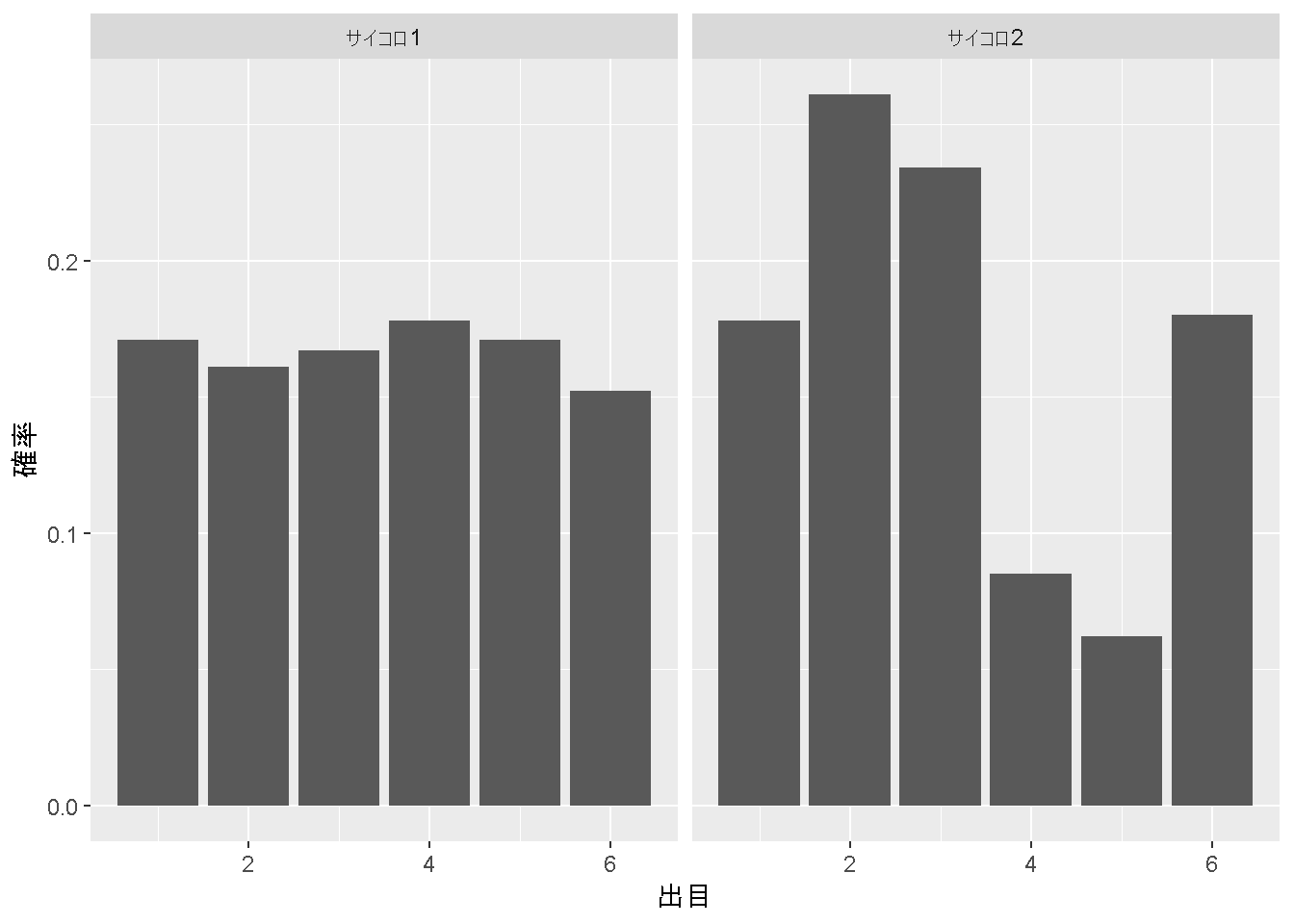
これが、サイコロ1とサイコロ2の(なんちゃって)確率分布です。
(サイコロ1の出目、$X_1$や、サイコロ2の出目$X_2$のことを、確率変数といいます。)
ここで、「なんちゃって」確率分布と言っているのは、「本当の確率分布」の値と違うからです。
このデータを生成した関数の内容を私たちは知っています。
再掲すると、
roll1 <- function(){
sample(1:6,1)
}
roll2 <- function(){
sample(1:6,1,prob = c(2,3,3,1,1,2))
}なので、実際の$P(X_1=出目)$と$P(X_2=出目)$は、
| 出目 | $P(X_1=出目)$ | $P(X_2=出目)$ |
|---|---|---|
| 1 | $\frac{1}{6}$ | $\frac{2}{12}$ |
| 2 | $\frac{1}{6}$ | $\frac{3}{12}$ |
| 3 | $\frac{1}{6}$ | $\frac{3}{12}$ |
| 4 | $\frac{1}{6}$ | $\frac{1}{12}$ |
| 5 | $\frac{1}{6}$ | $\frac{1}{12}$ |
| 6 | $\frac{1}{6}$ | $\frac{2}{12}$ |
となることを、私たちは知っています。
こっちが、本当の確率分布です。
10万回振ってみる
さて、1,000回ずつサイコロを振った状態で、なんちゃって確率分布を求めることができました。でも、真の分布からすると、ちょっとした「ずれ」が目立ちます。なので、100,000回サイコロを振ってみましょう。
result1 <- map_int(1:100000,~{roll1()})
result2 <- map_int(1:100000,~{roll2()})
dice1 <- ggplot() +
geom_bar(aes(x = result1)) +
labs(x = “サイコロ1の結果”, y = “回数”)
dice2 <- ggplot() +
geom_bar(aes(x = result2)) +
labs(x = “サイコロ2の結果”, y = “回数”)
cowplot::plot_grid(dice1,dice2)
そうして観測された確率と真の確率を比較してみると・・・
```r
hyou1 <- result1 %>%
enframe() %>%
count(value) %>%
mutate(total = sum(n)) %>%
mutate(p = n/total)
hyou2 <- result2 %>%
enframe() %>%
count(value) %>%
mutate(total = sum(n)) %>%
mutate(p = n/total)
bind_rows(
hyou1 %>% mutate(dice = "サイコロ1"),
hyou2 %>% mutate(dice = "サイコロ2")
) %>%
ggplot() +
geom_col(aes(x = value, y = p)) +
facet_wrap(~dice) +
labs(x = "出目", y = "確率")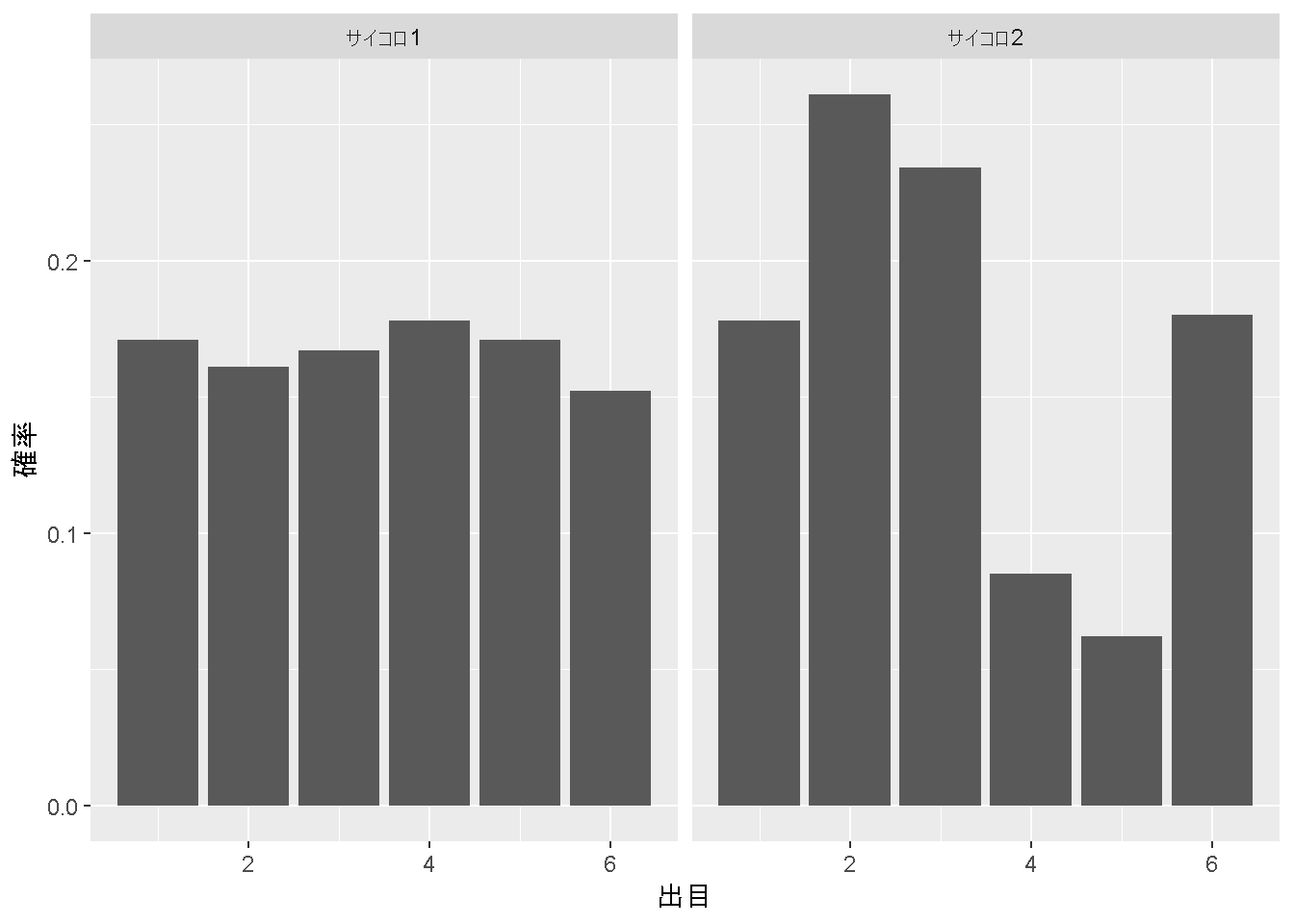
サイコロ1では、
hyou1_2 <- hyou1 %>%
mutate(total = sum(n)) %>%
mutate(p = n/total) %>%
mutate(realp = 1/6)
hyou1_2 %>%
knitr::kable(digits = 2, col.names = c("出目","回数","総試行回数","$観測されたP(X_1=出目)$","真の$P(X_1=出目)$"),
format.args = list(big.mark = ",",
scientific = FALSE))| 出目 | 回数 | 総試行回数 | $観測されたP(X_1=出目)$ | 真の$P(X_1=出目)$ |
|---|---|---|---|---|
| 1 | 171 | 1,000 | 0.17 | 0.17 |
| 2 | 161 | 1,000 | 0.16 | 0.17 |
| 3 | 167 | 1,000 | 0.17 | 0.17 |
| 4 | 178 | 1,000 | 0.18 | 0.17 |
| 5 | 171 | 1,000 | 0.17 | 0.17 |
| 6 | 152 | 1,000 | 0.15 | 0.17 |
サイコロ2では、
hyou2_2 <- hyou2 %>%
mutate(total = sum(n)) %>%
mutate(p = n/total) %>%
mutate(realp = c(2,3,3,1,1,2)/12)
hyou2_2 %>%
knitr::kable(digits = 2, col.names = c("出目","回数","総試行回数","$観測されたP(X_1=出目)$","真の$P(X_1=出目)$"),
format.args = list(big.mark = ",",
scientific = FALSE))| 出目 | 回数 | 総試行回数 | $観測されたP(X_1=出目)$ | 真の$P(X_1=出目)$ |
|---|---|---|---|---|
| 1 | 178 | 1,000 | 0.18 | 0.17 |
| 2 | 261 | 1,000 | 0.26 | 0.25 |
| 3 | 234 | 1,000 | 0.23 | 0.25 |
| 4 | 85 | 1,000 | 0.09 | 0.08 |
| 5 | 62 | 1,000 | 0.06 | 0.08 |
| 6 | 180 | 1,000 | 0.18 | 0.17 |
と、ほぼ一致しています。
いかさまサイコロの確率分布
さて、100000回、サイコロを振れば、より確からしく、サイコロ1とサイコロ2のどっちがいかさまサイコロか判別できると思います。ここで、どっちがいかさまかどうかを判断するのに検定の考え方が利用できます。が、ここでは、確率分布の話を続けましょう。(検定は別の機会に)
上の状況ではいかさまサイコロを関数を利用してシミュレーションをして、$P(X_2=出目)$の値を推定しました。
$$P(X_2=1) = \frac{2}{12}$$
$$P(X_2=2) = \frac{3}{12}$$
$$P(X_2=3) = \frac{3}{12}$$
$$P(X_2=4) = \frac{1}{12}$$
$$P(X_2=5) = \frac{1}{12}$$
$$P(X_2=6) = \frac{2}{12}$$
真の(離散)確率分布はこんな数式になります。
ここで、一つ重要な確率分布の性質をお伝えしておきます。
質問です。次の式の答えは何でしょうか?
$$
\sum_{X_1=1}^6{P(X_1)} = quad?
$$
実は、$P(X_1)$が確率分布だということがわかっているので、
上の数式は、
$$サイコロを振って1がでる確率+2が出る確率+cdots+6が出る確率$$
を意味します。
こう説明されると簡単ですね?
(6面の)サイコロを振って1、2、3、4、5、6以外の数字がでる可能性は0なので、1から6のいずれかの数字がでる確率は100%となり、
$$
\sum_{X_1=1}^6{P(X_1)} =
P(1) + P(2) + P(3) + P(4) + P(5) + P(6) =
\frac{1}{6} + \frac{1}{6} + \frac{1}{6} + \frac{1}{6} + \frac{1}{6} + \frac{1}{6} = \frac{6}{6} = 1
$$
おなじように、
$$
\sum_{X_1=1}^6{P(X_2)} =
P(1) + P(2) + P(3) + P(4) + P(5) + P(6) =
\frac{2}{6} + \frac{3}{6} + \frac{3}{6} + \frac{1}{6} +s \frac{1}{6} + \frac{2}{6} = \frac{6}{6} = 1
$$
と、確率分布で起こりうるすべての場合を足し合わせると1になります。
つづく。

コメント